万有引力 - 物理 - マナブスコープ

万有引力

ケプラーの法則・万有引力による位置エネルギー

ケプラーの法則

第1法則(楕円軌道の法則)

惑星は太陽を1つの焦点とする楕円軌道を描く。

第2法則(面積一定の法則)

惑星と太陽を結ぶ線分が単位時間に描く面積は一定である。

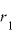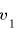太陽の周りを回る惑星の地点Aでの太陽との距離を $r_{1}$ 、速度を $v_{1}$ 、別の地点Bでの太陽との距離を 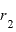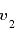$r_{2}$ 、 $v_{2}$ とすると、

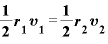
$\displaystyle \frac{\bm{1}}{\bm{2}}\bm{r}_{\bm{1}}\bm{v}_{\bm{1}}=\frac{\bm{1}}{\bm{2}}\bm{r}_{\bm{2}}\bm{v}_{\bm{2}}$

第3法則(調和の法則)

各惑星の公転周期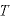 $T$ の2乗は、半長軸 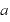$a$ の３乗に比例する。

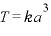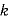$T=ka^{3}$ ( $k$ は定数)

すなわち太陽に近いほど惑星は速く回るということ。

万有引力の法則

2つの物体間にはひきつけあう力(万有引力)がはたらく。

万有引力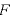 $F$ [N]の大きさは次の式で表される。

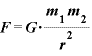
$\displaystyle \bm{F}=\bm{G}\mathbf{\cdot}\frac{\bm{m}_{\bm{1}}\bm{m}_{\bm{2}}}{\bm{r}^{\bm{2}}}$

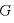$G$ [N･m²/kg²]:万有引力定数

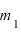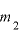$m_{1}$ ・ $m_{2}$ [kg]:物体１と物体2の質量

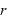$r$ [m]:物体1と物体2の距離

万有引力定数

万有引力定数(上の式の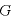 $G$ )はおよそ次の値である。

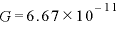$G=6.67\times 10^{-11}$ N･m²/kg²

万有引力と重力

重力=万有引力+遠心力

ただし、遠心力はたいていの場合極小であるため、重力≒万有引力である

よって、地球の質量を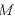 $M$ 、物体の質量を 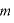$m$ とすると、
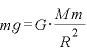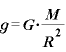
$mg=G\displaystyle \cdot\frac{Mm}{R^{2}}$ より、 $\displaystyle \bm{g}=\bm{G}\mathbf{\cdot}\frac{\bm{M}}{\bm{R}^{\bm{2}}}$

この式は、万有引力の問題で、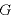 $G$ が与えられずに 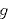$g$ が与えられているときに有効である。

万有引力による位置エネルギー

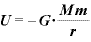
$\displaystyle \bm{U}=-\bm{G}\mathbf{\cdot}\frac{\bm{M}\bm{m}}{\bm{r}}$

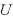$U$ [J]:万有引力による位置エネルギー(基準点は無限円)

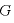$G$ [N･m²/kg²]:万有引力定数

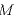$M$ [kg]:地球の質量

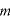$m$ [kg]:物体の質量

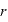$r$ [m]:地球の中心と物体との距離

※万有引力による位置エネルギーは基準点を無限円に設定するので、マイナスがつく

なお、万有引力の問題には、等速円運動の公式(→円運動)を用いる問題もある。