単振動
速度・加速度・位相
振幅を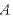 [m]、周期を
[m]、周期を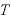 [s]、振動数を
[s]、振動数を [Hz]とすると、
[Hz]とすると、
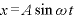
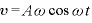
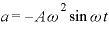
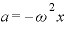
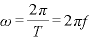
なお、角度を表す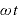 の部分を位相という。
の部分を位相という。
復元力
元の状態に戻ろうとする力
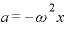 を運動方程式
を運動方程式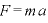 に代入すると、
に代入すると、
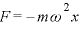
∴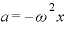
※この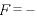 ○
○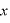 の形は復元力を表す
の形は復元力を表す
単振動の問題を解く手順
単振動の問題では、原点を力のつりあう位置とする。
1.運動方程式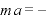 ○
○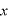 をたてて、それを
をたてて、それを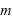 でわって
でわって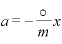 ・・・①の形に
・・・①の形に
2.①と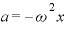 を比較して
を比較して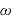 を求める。
を求める。
水平ばね振り子
振動の中心をつりあいの位置として考える。
ばね定数を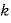 、振幅を
、振幅を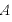 とすると、
とすると、
位置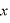 について運動方程式を立てて、
について運動方程式を立てて、
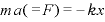 ←単振動の式
←単振動の式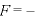 ○
○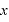 の形
の形
両辺を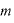 で割って、
で割って、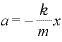 ・・・①
・・・①
①を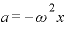 を比較して、
を比較して、
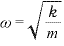
鉛直ばね振り子
振動の中心をつりあいの位置(静止した状態の位置)として考える。
ばねにおもりをつるして静止した状態の自然長からの伸びを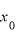 、ばね定数を
、ばね定数を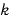 とすると、
とすると、
つりあいの式を立てて、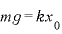 ・・・① ∴
・・・① ∴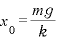
おもりが位置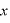 のとき、運動方程式を立てて、
のとき、運動方程式を立てて、
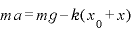
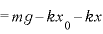
この式に①の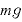 を代入して、
を代入して、
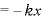 ←単振動の式
←単振動の式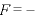 ○
○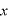 の形
の形
両辺を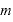 で割って、
で割って、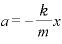 ・・・①
・・・①
①を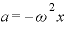 を比較して、
を比較して、
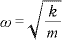
単振り子
長さ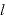 の単ふち子において、
の単ふち子において、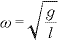 となる。
となる。
周期は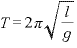 となり、この式から周期は振り子のおもりの重さによらないことが分かる。これを振り子の等時性という。
となり、この式から周期は振り子のおもりの重さによらないことが分かる。これを振り子の等時性という。
単振動のエネルギー
ばねの位置エネルギーは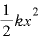 であらわされるので、
であらわされるので、
力学的エネルギー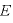 は
は
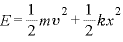 とあらわされる。
とあらわされる。
ここで、単振動の式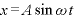 、
、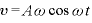 を代入すると、
を代入すると、
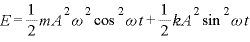
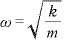 より、
より、
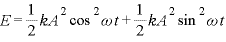
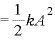 (
(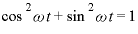 より)
より)
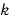 、
、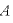 は定数であるので、力学的エネルギーは保存することが分かる。
は定数であるので、力学的エネルギーは保存することが分かる。
単振動による力学的エネルギーは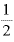 ○
○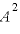 の形で表される。
の形で表される。
浮力による単振動
浮力は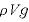 であらわされる(→圧力と浮力)ので、運動方程式を立て、
であらわされる(→圧力と浮力)ので、運動方程式を立て、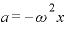 と比較して
と比較して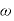 を求める。
を求める。