静電誘導・誘電分極
電荷と静電気力
電荷・・・電気現象を生じさせるもの。正電荷と負電荷がある。
同符号の電荷は互いに斥力、異符号の電荷は互いに引力を生じる。
電気量・・・電荷が持つ電気の量。単位はクーロン(C)。
帯電・・・物体内の+と≠フバランスが崩れたことにより電気を帯びること。
静電誘導・誘電分極
たとえば、物体の上側に負の電気を帯びた帯電体を近づけると、
導体は、自由電子を持つため、物体の上側に正、下側に負の電気が集まる。この現象を静電誘導という。
一方、不導体は自由電子を持たないため、構成粒子の中に電子は束縛されている。そのため、粒子の中で+が上側、-が下側を向くようになる。個の現象を誘電分極という。
電気量保存
導体に帯電体を近づけても、直接触れなければ、電荷がその同体内を移動するだけで、電荷の総量は一定である。
はく検電器
アース(接地)
はく検電器が開いた状態(はくの電荷が偏った状態)で、金属板を人間が触れると、偏っていた電子が体のほうに逃げるため、はくが閉じる。このとき、触れた人間は非常に多くの電子を持つ導体で、触れることで電荷の調整が起こったと考えることができる。このような大きな導体に電気を逃がすことをアース(接地)という。
静電遮へい
はく検電器を金網などの導体で覆うと、外から帯電体を近づけてもはくは影響を受けない。これは金網内の電子が移動することで影響を打ち消しあっているからであり、このような現象を静電遮へいという。
クーロンの法則と電場
クーロンの法則
2つの点電荷間に働く静電気力を求めることができる。
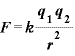
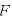 [N]:静電気力の大きさ
[N]:静電気力の大きさ
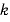 [N・m2/C2]:クーロンの法則の比例定数(真空中では
[N・m2/C2]:クーロンの法則の比例定数(真空中では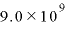 N・m2/C2)
N・m2/C2)
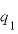 ,
,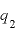 [C]:2つの点電荷の電気量の大きさ
[C]:2つの点電荷の電気量の大きさ
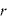 [m]:点電荷間の距離
[m]:点電荷間の距離
電場
物体が静電気力を受けるとき、その物体がある空間には電場が生じているという。
電場は、試験電荷(+1Cの電荷)がその場所で受ける静電気力であらわす。
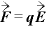
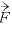 [N]:静電気力
[N]:静電気力
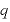 [C]:電気量
[C]:電気量
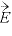 [N/C]:電場
[N/C]:電場
点電荷の作る電場
電場を知るときは、試験電荷をおけばいいので、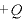 [C]点電荷の作る電場を調べるときは、調べたい地点に+1Cの点電荷をおく。すると、この+1Cの点電荷が受ける静電気力(すなわち電場)は、クーロンの法則より
[C]点電荷の作る電場を調べるときは、調べたい地点に+1Cの点電荷をおく。すると、この+1Cの点電荷が受ける静電気力(すなわち電場)は、クーロンの法則より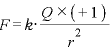 より、次の式が得られる
より、次の式が得られる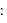
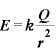
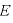 [N/C]:電場の強さ
[N/C]:電場の強さ
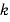 [N・m2/C2]:クーロンの法則の比例定数(真空中では
[N・m2/C2]:クーロンの法則の比例定数(真空中では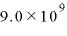 N・m2/C2)
N・m2/C2)
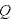 [C]:点電荷の電気量の大きさ
[C]:点電荷の電気量の大きさ
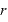 [m]:点電荷からの距離
[m]:点電荷からの距離
なお、複数の点電荷があるときは、それぞれの電荷からの電場を別々に考え、ベクトルの合成の要領で合成する。
電気力線とガウスの法則
電気力線・・・電場の形状をイメージした線
電気力線のルール
1. 正→負(電荷がないときは無限遠が電荷0として考える)の向き(+電荷で湧き出し、%d荷で吸い込む)。
2. 電荷のないところで発生・消滅しない。
3. 電気力線の接線は電場の方向に一致する。よって、折れ曲がったり、枝分かれしたり、交差したりしない(←接線が求められない)。
4. 電場が強いところほど密、弱いところほど疎。
電気力線の本数と電場
電気力線は、その場所の電場の強さが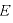 のとき、1m2あたりに
のとき、1m2あたりに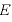 本描くという決まりであるため、次の式が得られる:
本描くという決まりであるため、次の式が得られる:
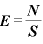 →
→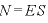
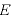 [N/C]:電場の強さ
[N/C]:電場の強さ
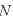 [本]:電気力線の本数
[本]:電気力線の本数
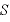 [m2]:電気力線が貫く表面積
[m2]:電気力線が貫く表面積
言い換えると、電場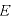 は、電気力線の本数密度であるともいえる。
は、電気力線の本数密度であるともいえる。
電気力線の本数とガウスの法則
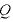 [C]の点電荷から出た電気力線は放射状になるため、点電荷から距離
[C]の点電荷から出た電気力線は放射状になるため、点電荷から距離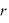 の地点を結ぶと球面になる。個の表面積は
の地点を結ぶと球面になる。個の表面積は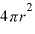 であるので、これを
であるので、これを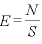 に代入すると、電気力線の本数
に代入すると、電気力線の本数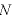 は次の式で表される:
は次の式で表される:
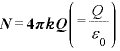
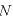 [本]:電気力線の本数
[本]:電気力線の本数
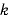 [N・m2/C2]:クーロンの法則の比例定数(真空中では
[N・m2/C2]:クーロンの法則の比例定数(真空中では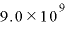 N・m2/C2)
N・m2/C2)
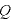 [C]:電荷の電気量
[C]:電荷の電気量
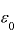 :誘電率
:誘電率
なお、この式は、電荷の形状に無関係に使用できることが知られている(ガウスの法則)。
ガウスの法則の使い方
1. 電荷と電場を求めたい点の間の距離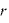 を調べる
を調べる
2. 電荷との距離が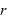 である面を想定する
である面を想定する
3. 2の面の内側にある電気量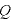 を求める
を求める
4. 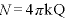 と
と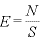 の式を使う
の式を使う
なお、2の面が球だった場合は、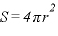 であるため、結局
であるため、結局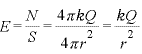 となり、点電荷の作る電場の式と同じになる。
となり、点電荷の作る電場の式と同じになる。
電位と電場
電位
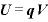
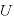 [J]:静電気力による位置エネルギー
[J]:静電気力による位置エネルギー
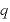 [C]:電気量
[C]:電気量
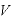 [V]:電位
[V]:電位
また、電場と力の関係は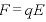 であるので(上記)、+と-の帯電体がが
であるので(上記)、+と-の帯電体がが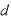 [m]離れているとき、その間の一様な電場が作る、静電気力のする仕事は
[m]離れているとき、その間の一様な電場が作る、静電気力のする仕事は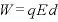 となる。
となる。
この仕事が位置エネルギーと同じだけの大きさと考えられるので、電位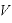 は、次の式で表される:
は、次の式で表される:
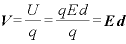
静電気力による位置エネルギー
位置エネルギー
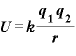
また、試験電荷(1C)をおいたときの位置エネルギーが電荷であるので、