ボイル・シャルルの法則
ボイルの法則
温度が一定のとき、一定の質量の気体の体積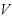 は圧力
は圧力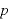 に反比例する。
に反比例する。
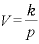 (
(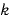 は比例定数)
は比例定数)
すなわち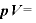 (一定)
(一定)
シャルルの法則
気体の温度を1[K]あげると、体積は0℃のときの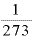 増加する。
増加する。
すなわち、圧力が一定のとき、一定の質量の気体の体積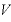 は絶対温度
は絶対温度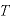 に比例する。
に比例する。
よって、温度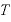 [K]における物体の体積
[K]における物体の体積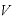 は、
は、
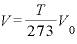
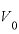 :0℃のときの物体の体積
:0℃のときの物体の体積
したがって、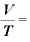 (一定)ということになる。
(一定)ということになる。
ボイル・シャルルの法則
ボイルの法則とシャルルの法則を合わせると、
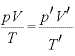 (
(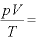 (一定))
(一定))
※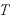 、
、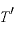 は絶対温度
は絶対温度
なお、状態変化せずに(途中で液体などにならずに)この法則に従う気体を理想気体という。
理想気体の状態方程式
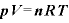
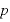 [Pa]:圧力
[Pa]:圧力
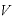 [m3]:体積
[m3]:体積
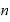 [mol]:物質量
[mol]:物質量
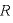 [J/(mol・K)]:気体定数
[J/(mol・K)]:気体定数
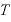 [K]:絶対温度
[K]:絶対温度
なお、気体定数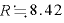 [J/(mol・K)]である。
[J/(mol・K)]である。
気体分子運動論
気体分子が、いっぺんの長さが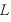 の立方体の容器の壁と弾性衝突するものとする。
の立方体の容器の壁と弾性衝突するものとする。
1つの気体分子が壁に与える力
1つの気体分子の運動の速度のうち、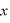 軸方向の速度を
軸方向の速度を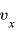 とすると、
とすると、
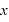 軸に垂直な壁Sとの衝突の前後で運動量の変化は
軸に垂直な壁Sとの衝突の前後で運動量の変化は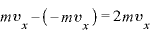 (←後の運動量-前の運動量。弾性衝突なので壁にぶつかると
(←後の運動量-前の運動量。弾性衝突なので壁にぶつかると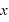 軸方向の速度は
軸方向の速度は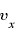 から
から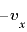 になる)。
になる)。
s
よって、壁に与える力積の大きさは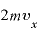 となる(運動量の変化=力積)。
となる(運動量の変化=力積)。
壁Sに再び衝突する(すなわち衝突して跳ね返ったあと、反対側の壁にぶつかってまた戻ってくる)までの時間は、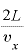 である。
である。
よって、1秒間に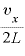 [回]衝突するので、
[回]衝突するので、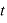 秒間にこの分子は壁に
秒間にこの分子は壁に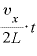 [回]衝突することになる。
[回]衝突することになる。
ゆえに、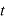 秒間にこの分子が壁に与える力の合計は
秒間にこの分子が壁に与える力の合計は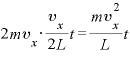 である。
である。
力積=力×時間であるので、1つの気体分子が壁に与える力の大きさ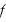 は、
は、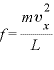
気体分子の平均速度
気体分子1個の速度は
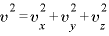 (←三平方の定理より)
(←三平方の定理より)
多数の分子のとき、その平均速度についても
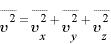
分子の個数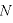 は非常に大きく、すべての分子は方向に偏りなく不規則に運動するから、どの方向の平均値も等しいと考えられるため、
は非常に大きく、すべての分子は方向に偏りなく不規則に運動するから、どの方向の平均値も等しいと考えられるため、
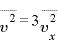 (←
(←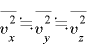 )
)
よって、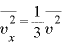
壁SがN個の気体分子から受ける圧力
気体分子1個が壁Sに与える力の大きさを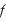 とすると、
とすると、
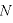 個の気体分子が壁Sに及ぼす力の大きさ
個の気体分子が壁Sに及ぼす力の大きさ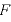 は、
は、
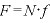
壁Sの面積は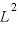 であるので、壁Sが
であるので、壁Sが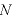 個の気体分子から受ける圧力
個の気体分子から受ける圧力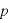 は、
は、
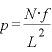 (←圧力
(←圧力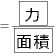 )となる。
)となる。
ここで、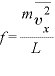 であるので
であるので
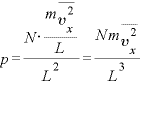
さらに、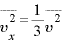 であるので、
であるので、
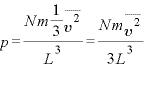
また、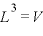 なので、
なので、
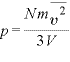 すなわち
すなわち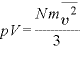
なお、球形容器における気体分子運動論でも、同様の結果が得られる。
気体の内部エネルギー
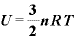
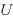 [J]:内部エネルギー
[J]:内部エネルギー
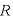 [J/(mol・K)]気体定数
[J/(mol・K)]気体定数
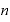 [mol]:物質量
[mol]:物質量
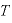 [K]:絶対温度
[K]:絶対温度
なお、温度が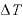 [K]上昇したときの内部エネルギーの変化
[K]上昇したときの内部エネルギーの変化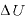 は
は
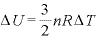
定圧変化
熱力学第一法則
物体に与えた熱量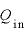 [J]と、物体にした仕事
[J]と、物体にした仕事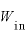 [J]の和は、物体の内部エネルギーの変化
[J]の和は、物体の内部エネルギーの変化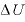 [J]に等しい
[J]に等しい
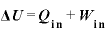 (
(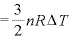 )
)
QinとQout、WinとWoutの関係
気体に与えた熱量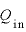 [J]と、気体が排出した熱量
[J]と、気体が排出した熱量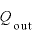 の関係は、
の関係は、
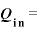
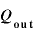
気体にした仕事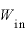 [J]と気体が外にした仕事
[J]と気体が外にした仕事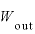 の関係は、
の関係は、
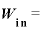
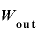
定圧変化
定圧変化・・・圧力を一定に保った変化
気体が外にする仕事は
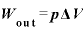
内部エネルギーの変化は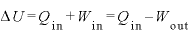 なので、
なので、
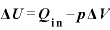
定積変化
定積変化・・・体積が一定のときの変化
定圧変化では、体積が変化しないので、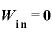
よって、熱力学第1法則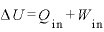 より、
より、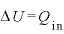
ゆえに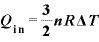
等温変化
等温変化・・・温度を一定に保ったときの変化
すなわち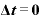 であり、内部エネルギー
であり、内部エネルギー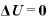
ここで、熱力学第1法則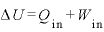 より、
より、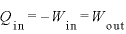
すなわち加えられた熱がすべて仕事になる。
断熱変化
断熱変化・・・熱の出入りがない変化(外部から熱を加えたり、冷やしたりしない)
すなわち外部から力を加えて(仕事をして)体積を変化させる変化。
よって、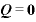
ここで、熱力学第1法則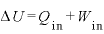 より
より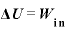
体積を大きくするとき(断熱膨張)
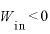 なので、
なので、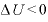
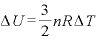 であり、
であり、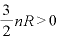 なので、
なので、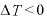
よって、体積を大きくすると、温度は下がる。
体積を大きくするとき(断熱膨張)
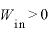 なので、
なので、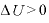
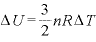 であり、
であり、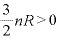 なので、
なので、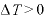
よって、体積を小さくすると、温度は上がる。
熱効率
熱効率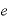 ・・・熱機関の効率の良さを表す。数字が大きいほど効率がよい。
・・・熱機関の効率の良さを表す。数字が大きいほど効率がよい。
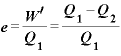
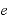 :熱効率
:熱効率
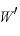 [J]:熱機関がする仕事
[J]:熱機関がする仕事
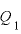 [J]:高温の物体から吸収する熱量
[J]:高温の物体から吸収する熱量
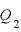 「J]:低音の物体へ放出する熱量
「J]:低音の物体へ放出する熱量
すなわち熱効率
なお、一般的に熱効率は蒸気機関で0.1~0.2、ガソリン機関では0.2~0.3、ディーゼル機関で0.3~0.4程度である。
モル比熱
モル比熱
モル比熱・・・1molの気体の温度を1K上げるのに必要な熱量。
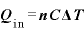
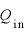 [J]:気体が吸収する熱量
[J]:気体が吸収する熱量
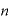 [mol]:気体の物質量
[mol]:気体の物質量
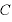 [J/(mol・K)]:モル比熱
[J/(mol・K)]:モル比熱
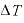 [K]:期待の温度変化
[K]:期待の温度変化
定積モル比熱
定積モル比熱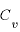 ・・・定積変化する際のモル比熱。
・・・定積変化する際のモル比熱。
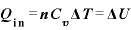 (←
(←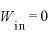 なので、
なので、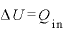 )
)
なお、単原子分子では、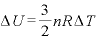 より、
より、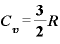
※2原子分子では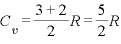 (←3次元の動きに加え、縦・横の回転を加えた)
(←3次元の動きに加え、縦・横の回転を加えた)
定圧モル比熱
定圧モル比熱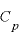 ・・・定圧変化するときのモル比熱
・・・定圧変化するときのモル比熱
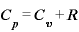 (←マイヤーの関係)
(←マイヤーの関係)
求め方
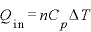 より
より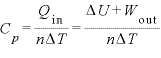 (←
(←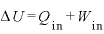 より
より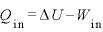 )
)
ここで、定圧変化では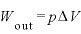 なので、
なので、
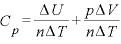
また、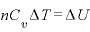 より
より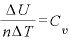 であり、
であり、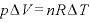 より
より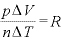 であるので、
であるので、
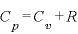
比熱比
比熱比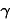 ・・・定圧モル比熱と定積モル比熱の比。
・・・定圧モル比熱と定積モル比熱の比。
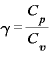
なお、単原子分子の場合は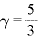 となる
となる
ポアソンの法則
断熱変化するとき、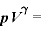 (一定)
(一定)
不可逆変化
不可逆変化・・・外から操作をしない限り、元の状態に戻すことができない変化。
一般に、熱が関与する変化は不可逆変化である。